Visualiseren van progressie

Visualiseren kan een sterk motiverend effect hebben . Hier zijn enkele suggesties voor hoe je gebruik kunt maken van visualisaties.

Hoofdboodschap: verwacht fluctuatie en hou de trendlijn in de gaten

Progressie verloopt vrijwel nooit in een rechte lijn. Het plaatje rechts toon een voorbeeld uit de praktijk van een verbeterproces. De dikke lijn laat de werkelijke waarden zien die gevonden werden (bijvoorbeeld verkoopcijfers op een bepaald moment in de tijd). Zoals je ziet fluctueren de niveaus steeds. De dunne lijn is de trendlijn die laat zien dat er over de hele periode bezien een langzame maar zekere verbetering plaatsvindt. De pijlen laten het volgende zien: Pijl 1: snelle eerste resultaten, snelle progressie. Pijl 2: een behoorlijke terugval. Pijl 3: opnieuw een snelle verbetering. Pijl 4: opnieuw een ernstige terugval waarna de verbeteringen weer beginnen. Het zou heel gemakkelijk zijn om ontmoedigd te raken als je teveel let op de fluctuaties, bijvoorbeeld bij punt 2 en punt 4. Twee dingen zijn belangrijk om te onthouden: 1) het is normaal dat progressie dit soort fluctuatie vertoond en 2) De trendlijn is belangrijk om in de gaten te houden. Deze lijn laat zien dat er per saldo sprake is van vooruitgang. De trendlijn is een motiverende lijn om te blijven volgen.

Kijk wiskundig naar progressie

Een kort intermezzo voordat we gaan naar de tweede boodschap over visualiseren van progressie. Enkele jaren geleden schreef hoogleraar wiskunde en auteur Steven Strogatz twee columns in de New York Times met als titels Change We Can Believe In en It Slices, It Dices. De columns gaan over de tak van de wiskunde die Analyse heet (in het Engels wordt dit ‘calculus’ genoemd). Analyse gaat over limieten, functies, afgeleiden, integralen en oneindige reeksen.  Analyse is de wiskunde van verandering. De twee belangrijkste onderdelen van de Analyse zijn differentiaalrekening (werken met afgeleiden) en integraalrekening. Zonder een diepgaande uitleg te geven over deze onderwerpen volgt hier een korte introductie.

Differentiaalrekening is de studie van de afgeleiden van functies. Het berekenen van een afgeleide heet differentiëren. De afgeleide vertelt je hoe snel iets verandert, hoeveel je omhoog of omlaag gaat op lijn die de functie weergeeft. De afgeleide is de benadering van de helling van de grafiek. De afgeleide kan worden berekend voor elk afzonderlijk punt van de functie maar ook voor de functie als geheel wat leidt tot de afgeleide functie (zie het plaatje rechts [van www.derivate.it]). Wanneer een helling omhoog gaat is de afgeleide positief; wanneer de helling omlaag gaat is hij negatief. Op de top en de bodem van de curve is de afgeleide nul. Op deze punten staat de verandering tijdelijk stil.

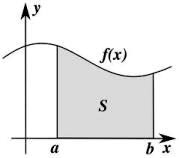Integraalrekening is de studie van integralen die wordt gebruikt om te bepalen hoe snel iets accumuleert. Het is de analyse van de optelling. Het berekenen van een integraal komt neer op het meten van het gebied onder de curve (zie het plaatje links). Functies kunnen heel onregelmatige vormen hebben wat het tamelijk lastig kan maken om dit gebied onder de curve te meten of berekenen. Integraalrekening lost dit probleem op door het gebied in dunne plakjes op te delen, het volume van die plakjes te berekenen en deze dan slim bij elkaar op te tellen. (Terzijde integraalrekening is de inverse bewerking van differentiaalrekening).

Tweede boodschap: kijk naar de helling en de accumulatie

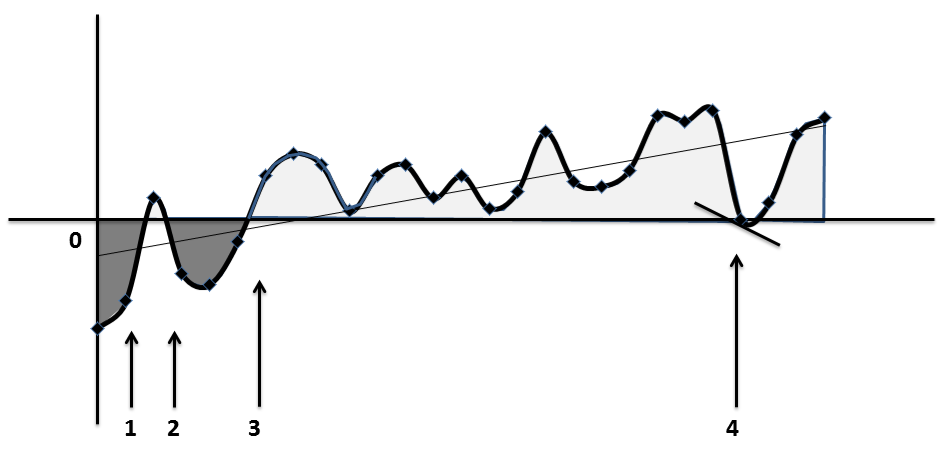Wanneer we de principes van afgeleiden en integralen toepassen op de originele grafiek krijgen we het plaatje rechts. Laten we deze principes toepassen op het in potentie meest deprimerende punt van de grafiek, punt 4. Het korte lijnstuk toont de afgeleide van punt vier, de gearceerde gebieden tonen de integraal van de grafiek tot aan punt 4. Beide geven reden voor een positieve en hoopvolle blik op de veranderresultaten. De afgeleide bij punt 4 laat zien dat de dingen nog steeds slechter worden maar de teruggang gaat langzamer wat hoop geeft dat de bodem in zicht is en dat een ommekeer er mogelijk aan zit te komen.  De gearceerde gebieden tonen de opbrengsten.  Het donker gearceerde gebied visualiseert de accumulatie van alles dat bereikt is tussen punt 0 en 3. Zoals je kunt zien blijven alle punten beneden 0 dus het resultaat is negatief. Het licht gearceerde gebied visualiseert de accumulatie van alles wat bereikt is tussen punt 3 en punt 4. Hoewel bij punt 4 de waarde van de functie weer 0 is is het netto resultaat van de verandering positief omdat het lichte gebied veel groter is dan het donkere gebied. Er is veel bereikt. De gedachte, bij punt 4, dat alle inspanningen voor niets zijn geweest, zou onterecht zijn. Er is heel wat bereikt en vooruitgang.